GRAFIK to mój graficzny program autorski, którego możliwości są ograniczone tylko do kształtów tworzonych figur.
Program tworzy kształt z kresek pionowych, poziomych, także ukośnych i łuków (w zmodyfikowanym dodatkowo programie)
Ww. kreski (długość 's', parametr w programie Grafik) zakodowane są z wykorzystaniem cyfr od 1 do 8 następująco:
0 - . . (w prawo przerwa)
1 - | (w dół)
2 - ---- (w prawo)
3 - | (w górę)
4 - ---- (w lewo )
5 - \ ( w prawo w dół)
6 - / (w lewo w dół)
7 - \ (w lewo w górę)
8 - / (w prawo w górę)
Gdy 's' = 30px, kwadrat 90px x 90px

zakodować można wektorem:
[1,1,1,2,2,2,3,3,3,4,4,4], albo
[1,2,3,4] gdy s = 90px
Dodatkowo zmodyfikowanym programem Grafik namalować można bardziej skomplikowane kształty:
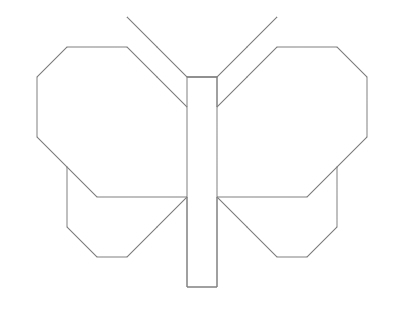
motyl
drzewo

wektor:
[6,6,2,6,6,6,2,2,2,6,6,6,2,2,2,2,1,1,3,3,2,2,2,2,7,7,7,2,2,2,7,7,7,2,7,7,7];
W zasadzie programem Grafik namalować można również każdy kształt, co będzie wiązać się z potrzebą powtarzania pewnych linii.
Do znalezienia optymalnych 'przejść', można wykorzystać zasady teorii grafów, ale już tylko dla ćwiczeń formalnych.
Graf, który ma drogę Eulera, ma albo dwa wierzchołki stopnia nieparzystego, albo nie ma w ogóle wierzchołków stopnia nieparzystego.
Motyl, a dokładnie graf zbudowany na jego bazie, nie ma drogi Eulera, ponieważ w grafie jest 8 wierzchołków stopnia nieparzystego, są to:
w. 1, w. 2, w. 3, w. 4, w.7, w.8, w.9, w.10.
zatem nie da się wyznaczyć wszystkich krawędzi motyla, bez powtórzeń.
Program GRAFIK namalował kształt motyla:
Tzw. drogę Eulera można wytyczyć na zewnętrznych krawędziach motyla,
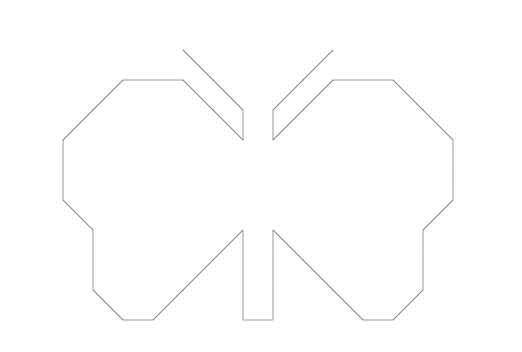
co namalować da się programem GRAFIK, wg danych z wektora:
[6,6,1,8,8,2,2,5,5,1,1,6,1,1,6,4,7,7,7,1,1,1,4,3,3,3,6,6,6,4,7,3,3,7,3,3,8,8,2,2,5,5,3,7,7]
Programem kratka można wydrukować siatkę linii, która na pewno ułatwi czynność tworzenia wektora.